You don’t get average returns when you make an investment. This is a very important concept. The reason it is important is that most mutual funds and ETFs will list average returns, but as an investor you never get the average return.
Simple Example
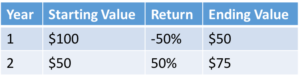Let’s illustrate this point with a simple example. Lets say you invest $100 and the investment loses 50% in year 1. Then in year 2, the investment goes up 50%.
Your average return is 0%.
But how much would the investment be worth?
Before I understood average returns I would have said $100. But the correct answer is $75. In order to get back to $100, after a 50% loss in year 1, the investment would need to go up by 100% in year 2.
What would it look like if you Did get the Average Return?
The average return of the S&P 500 between 2000 and 2015 was 5.71%.
Source: http://pages.stern.nyu.edu/~adamodar/New_Home_Page/datafile/histretSP.html
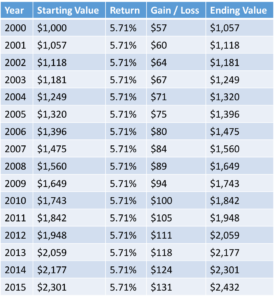But if you invested in the S&P 500 during that same timeframe you would not get the returns of 5.71% compounded annually.
If you got 5.71% interest each year, and you invested $1000 at the beginning of the year in 2000, by the end of the year in 2015 your $1,000 would have grown to $2,432.
This illustrates the power of compounding interest over time. Over 15 years this theoretical investment went up 143%.
However, an actual $1,000 investment in the S&P 500 would NOT have gone up this much.
The Return You Would Actually Get
I would love it if I invested $1,000 and it was worth $2,432 15 years later.
But that is not how much your investment would be worth if you invested $1,000 in the S&P 500 on 1 January 2000 and sold on 31 December 2015. Your $1,000 would be worth $1,877.
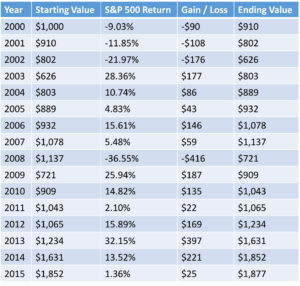The reason being that if an investment goes down, as the S&P 500 did 4 out of the 15 years during this period, it must go up by even more to make up for the losses.
It’s also worth noting that in order to get the $877 gain one would have to have held onto the investment through three consecutive years of losses over 9% and a 2008 drop of over 36%.
That would take an iron will.
The typical human reaction when faced with such losses is to sell to avoid further losses.
Why does the Financial Industry Use Average Annual Return?
The Vanguard 500 fund (VFINX) lists a 6.58% average annualized return over the past 10 years. If you really got 6.58% compounded each year the investment would roughly double in ten years, but this fund only went up about 50% over that timeframe.
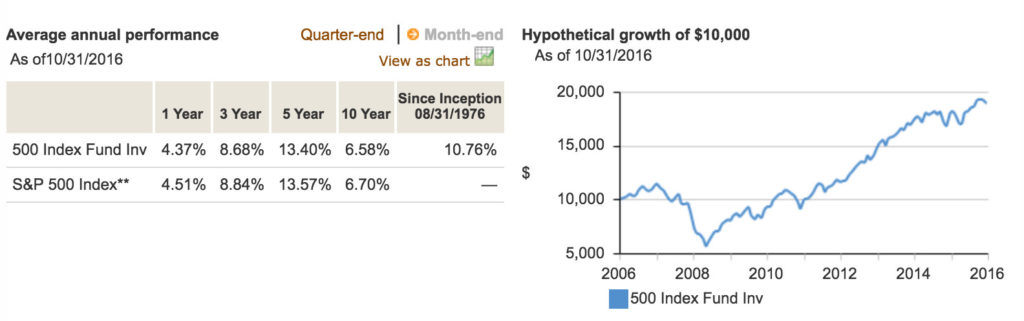
The main reason the average annualized return is used is probably because it makes the return of a fund look better than it actually is. Compound Annual Growth Rate (CAGR) would be a more useful and frankly honest metric because that is the rate an investor actually gets.
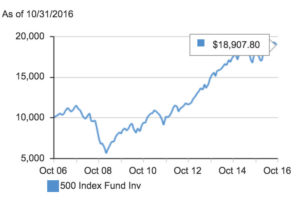I’m not trying to single out Vanguard. I think Vanguard is a good company but average annual performance is deceptive. And the chart on the right showing the hypothetical growth of $10,000 is also deceptive.
Source: https://personal.vanguard.com/us/funds/snapshot?FundId=0040&FundIntExt=INT
Why does it need to be hypothetical? We know exactly how much $10,000 invested in the VFINX in 2006 would be worth today. In October 2006 VFINX was trading at 122.62 and in October 2016 it was trading at 196.54. So a $10,000 investment would result in a gain of $6,028 for a total value of $16,028. But Vanguard lists the gain as $18,907.80 which would only be the case if this fund returned 6.58% compounded annually with no losses.
How Much Gain is Required to Recoup a Loss?
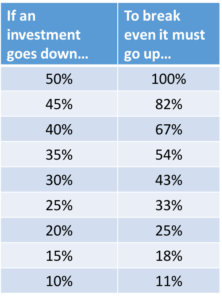The problem with losses is that when trying to make them up and get back to even you are doing so with less money.
Not surprisingly, the greater the loss, the greater the gain needed to make it up. With smaller losses the gain only has to be slightly larger to get back to break even. However, with larger losses, higher and higher multiple gains are needed to recoup the losses.
The moral of the story is that 1) you won’t get the average return for an investment, so when you see an average return listed for an ETF or Mutual fund, you can ignore it, it’s not a useful number 2) when an investment goes down in value, it is costly.